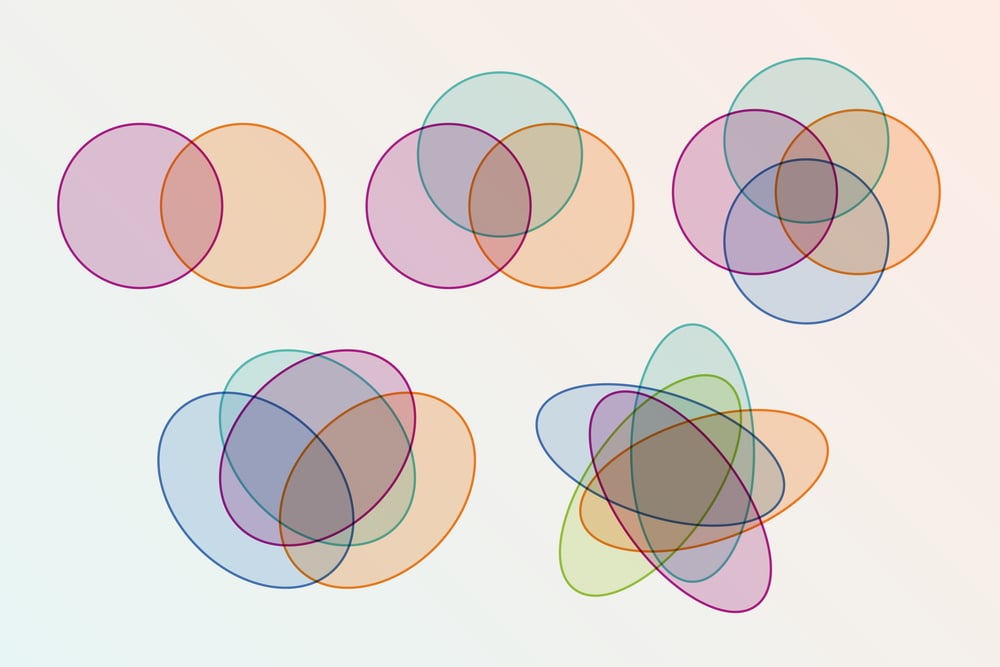Ellipse là một giải pháp mà các nhà khoa học tìm ra

4 hình tròn giao nhau chỉ có thể tạo ra 12 điểm giao, trong khi các ellipse nếu biết sắp xếp, chúng có thể tạo ra 14 điểm giao, phù hợp với số vùng với 4 hình

Một số nhà toán học chuyển sang hình dạng “ngoằn ngoèo” hơn hoặc thậm chí không gian ba chiều để giữ đủ số vùng cần thiết, nhưng những cách này đánh đổi sự trực quan vốn là ưu điểm của sơ đồ Venn.

Một bước ngoặt thú vị đến vào năm 1960 khi David W. Henderson, khi ấy còn là sinh viên đại học, phát hiện rằng: một sơ đồ Venn chỉ có thể đạt được tính đối xứng khi số tập hợp là một số nguyên tố – tức chỉ chia hết cho 1 và chính nó, như 2, 3, 5, 7 nhưng không phải 4. Điều này giải thích vì sao sơ đồ Venn với 2 hay 3 vòng tròn thì xoay vẫn giống hệt nhau, nhưng đến bốn hình ellipse thì lại mất đi tính đối xứng ấy.

Ngoài ra, Venn từng cho rằng không thể vẽ sơ đồ năm tập hợp bằng năm ellipse. Nhưng đến năm năm 1975, Branko Grünbaum chứng minh rằng vẫn có thể tạo sơ đồ đối xứng với năm tập hợp – phá tan niềm tin lâu nay rằng điều đó là bất khả. Và đến năm 2004, các nhà toán học từ Đại học South Carolina xác nhận rằng mọi số nguyên tố đều có thể tạo ra sơ đồ Venn đối xứng.